对称加密
本文讨论现代密码学中的对称加密。
对称加密技术有两种宽泛的类型:块密码(block cipher)和流密码(stream cipher)。块密码用在多种因特网协议的加密中,包括 PGP、SSL 和 IPsec 等;流密码用在无线 LAN 的安全性中。
块密码
在块密码中,要加密的报文被处理为 $k$ 比特的块。为了加密一个块,该密码采用了一对一映射,将 $k$ 比特块的明文映射为 $k$ 比特块的密文。
假设 $k=3$,因此块密码将 3 比特输入(明文)映射为 3 比特输出(密文)。下表给出了一种可能的映射:
| 输入/输出 | 比特块 | 比特块 | 比特块 | 比特块 | 比特块 | 比特块 | 比特块 | 比特块 |
|---|---|---|---|---|---|---|---|---|
| 输入 | 000 | 001 | 010 | 011 | 100 | 101 | 110 | 111 |
| 输出 | 110 | 111 | 101 | 100 | 011 | 010 | 000 | 001 |
可以验证,报文 010110001111 被加密成了 101000111001。
注意到上述映射只是许多可能映射中的一种,观察到一个映射只不过是所有可能输入的排列,共有 $2^3$(=8)种可能的输入(排列在“输入”栏中),这 8 种输入能够排列为 $8!=40320$ 种不同方式,因此共有 40320 种可能的映射。我们能够将这些映射的每种视为一个密钥,即如果 A 和 B 都知道该映射(密钥),它们能够加密和解密在它们之间发送的报文。
对这种密码的蛮力攻击即通过使用所有映射来尝试解密密文,为了挫败蛮力攻击,块密码通常使用大得多的块,由 64 比特甚至更多比特组成。注意到对于通常的 $k$ 比特块密码,可能映射数量是 $2^k!$,对于即使不大的 $k$ 值(如 $k=64$),这也是一个天文数字。
像上面这种在所有输入和输出之间提供了预先决定的映射的方法称为全表块密码,尽管全表块密码对于不大的 $k$ 值能够产生健壮的对称密钥加密方案,但这要求加密双方各维护一张具有 $2^k$ 个输入值的表,这是一个难以实现的任务。此外,如果加密双方要改变密钥,它们将不得不各自重新生成该表。
取而代之的是,块密码通常使用函数模拟随机排列表。下图显示了当 $k=64$ 时,这种函数的一个例子。
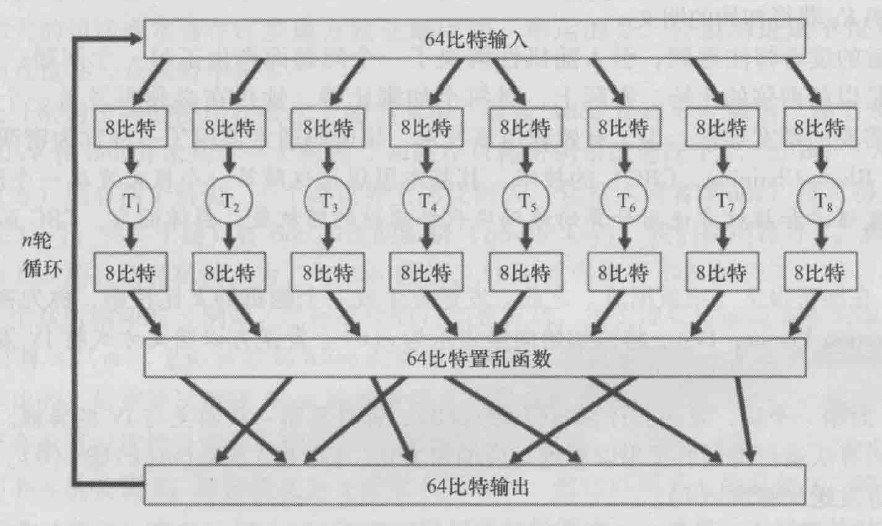
该函数首先将 64 比特块划分为 8 个块,每个块由 8 比特组成。每个 8 比特块由一个“8 比特到 8 比特”表处理,这是个可管理的长度。例如,第一个块由标志为 $T_1$ 的表来处理。接下来,这 8 个输出块被重新装配成一个 64 比特的块。该输出被回馈到 64 比特的输入,开始了第二次循环。经 n 次这样的循环后,该函数提供了一个 64 比特的密文块。这种循环的目的是使得每个输入比特影响最后输出比特的大部分(即使不是全部)。(如果仅使用一次循环,一个给定的输入比特将仅影响 64 输出比特中的 8 比特。)这种块密码算法的密钥将是 8 张排列表(假定置乱函数是公共已知的)。
目前有一些流行的块密码,包括 DES、3DES 和 AES 等。这些标准都使用了函数(而不是预先决定的表),连同上图中的线(虽然对每种密码来说更为复杂和具体)。这些算法也都使用了比特串作为密钥。一个算法的密钥决定了特定“小型表”映射和该算法内部的排列。
密码块链接
对于相同的块,块密码当然将产生相同的密文,这是不安全的,为了解决这个问题,可以在密文中混合某些随机性,使得相同的明文块产生不同的密文块。
在介绍其思想之前,先明确一些术语:令 $m(i)$ 表示第 $i$ 个明文块,$c(i)$ 表示第 $i$ 个密文块,并且 $a\oplus b$ 表示两个比特串 $a$ 和 $b$ 的异或(XOR),另外,将具有密钥 $S$ 的块密码加密算法表示为 $K_S$。
其基本思想如下:
发送方为第 $i$ 块生成一个随机的 $k$ 比特数 $r(i)$,并且计算 $c(i)=K_S(m(i)\oplus r(i))$。注意到每块选择一个新的 $k$ 比特随机数。则发送方发送 $c(1)$、$r(1)$、$c(2)$、$r(2)$、$c(3)$ 和 $r(3)$ 等等。因为接收方接收到 $c(i)$ 和 $r(i)$,它能够通过计算 $m(i)=K_S(c(i)\oplus r(i))$ 而恢复每个明文块。
尽管 $r(i)$ 是以明文发送的,但嗅探者无法获得明文 $m(i)$,因为它不知道密钥 $K_S$。如果两个明文块 $m(i)$ 和 $m(j)$ 是相同的,对应的密文块 $c(i)$ 和 $c(j)$ 将是不同的(只要随机数 $r(i)$ 和 $r(j)$ 不同,这种情况出现的概率将很高)。
举例来说,参照上表的 3 比特块密码,假设明文是 010010010,若直接加密,没有包括随机性,则密文为 101101101;若使用上述技术加密,假设生成了随机块 $r(1)=001$,$r(2)=111$ 和 $r(3)=100$,则生成的密文为 $c(1)=100$,$c(2)=010$ 和 $c(3)=000$。
引入随机性解决了一个问题而产生了另一个问题,即发送方必须传输以前两倍的比特。实际上,对每个加密比特,它现在必须再发送一个随机比特,使需要的带宽加倍。为了有效利用该技术,块密码通常使用了一种称为密码块链接(Cipher Block Chaining,CBC)的技术。其基本思想是 仅随第一个报文发送一个随机值,然后让发送方和接收方使用计算的编码块代替后继的随机数。具体而言,CBC 运行过程如下:
- 在加密报文(或数据流)之前,发送方生成一个随机的 $k$ 比特串,称为初始向量(Initialization Vector,IV)。将该初始向量表示为 $c(0)$。发送方以 明文方式 将 IV 发送给接收方。
- 对第一个块,发送方计算 $m(1)\oplus c(0)$,即计算第一块明文与 IV 的异或。然后通过块密码算法运行得到的结果以得到对应的密文块,即 $c(1)=K_S(m(1)\oplus c(0))$。发送方向接收方发送加密块 $c(1)$。
- 对于第 $i$ 个块,发送方根据 $c(i)=K_S(m(i)\oplus c(i-1))$ 生成第 $i$ 个密文块。
当接收方接收到 $c(i)$ 时,它用 $K_S$ 解密之以获得 $s(i)=m(i)\oplus c(i-1)$;因为接收方已经知道 $c(i-1)$,则从 $m(i)=s(i)\oplus c(i-1)$ 获得明文块。
举例来说,参照上表的 3 比特块密码,假设明文是 010010010,$IV=c(0)=001$,则 $c(1)=K_S(m(1)\oplus c(0))=100$,$c(2)=K_S(m(2)\oplus c(1))=K_S(010\oplus 100)=000$,$c(3)=K_S(m(3)\oplus c(2))=K_S(010\oplus 000)=101$。